
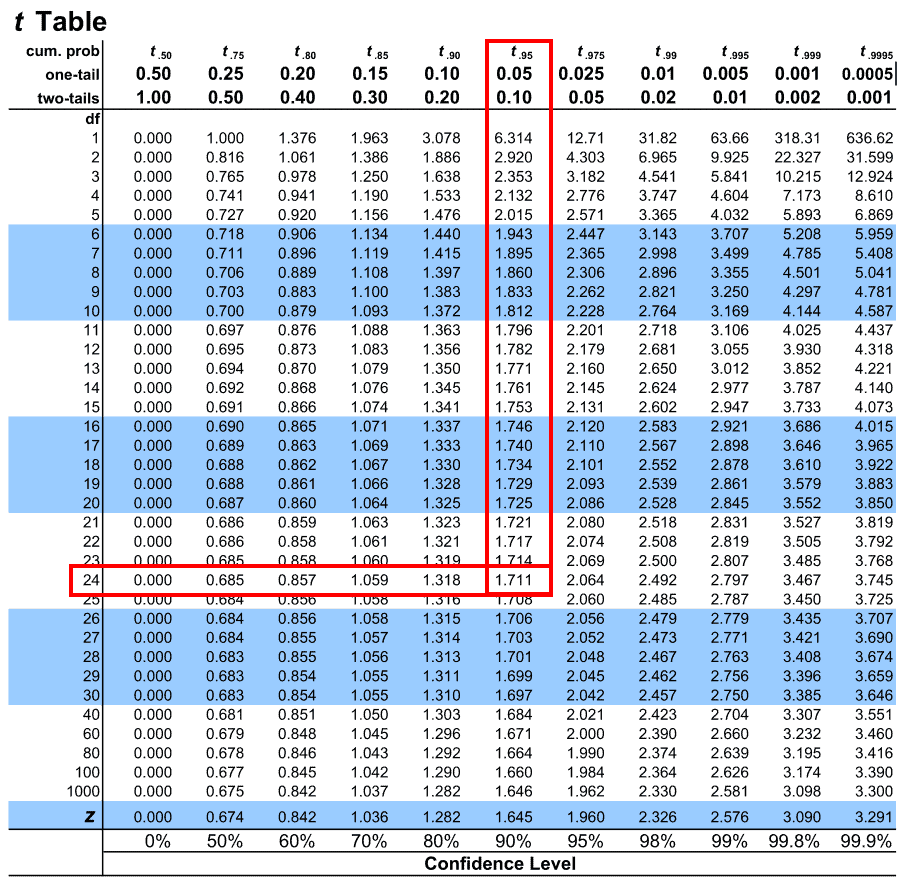
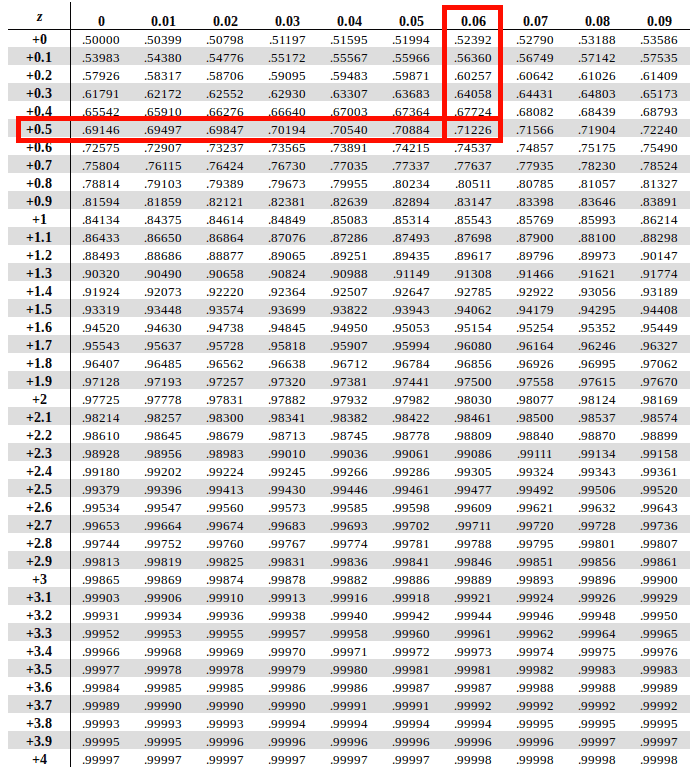
If the behavior of an estimator is taken as its variance, a given estimator may have minimum variance for the distribution used, but it may not be very good for the actual distribution. Formally, a statistical procedure is robust if its behavior is relatively insensitive to deviations from the assumptions on which it is based. However, if the choice of the underlying family of distributions is based on past experience, there is a possibility that the true population will be slightly different from the model used to derive the estimators. The estimators derived in this chapter are for particular parameters of a presumed underlying family of distributions. Tsokos, in Mathematical Statistics with Applications in R (Third Edition), 2021 5.10.2 Robust estimation This page uses Creative Commons Licensed content from Wikipedia ( view authors).Kandethody M. (2004) Elementary Statistics: Picturing the World, 清华大学出版社.To find 0.69, first look down the rows to find 0.6 and then across the columns to 0.09 and 0.7549 will be the result. The below table read by using the rows to find the first digit, and the columns to find the second digit of a Z-score. What is the probability that an average of three scores is 82 or less?.What is the probability that a student scores between 78 and 88?.If your table does not have negatives, use Prob(Z ≤ -1.20) = Prob(Z ≥ 1.20) = 1. What is the probability that a student scores a 74 or less?.What is the probability that a student scores a 90 or more?.What is the probability that a student scores an 82 or less?.If you are using an average, divide the standard deviation by the square root of the sample size.Ī professor's exam scores are approximately distributed normally with mean 80 and standard deviation 5. If X is a random variable from a normal distribution with mean μ and standard deviation σ, its Z-score may be calculated from X by subtracting μ and dividing by σ. Remember that 50% falls below and above 0.Ĭonverting from normal to standard normal If your table does not have negative values, use symmetry to find the answer.
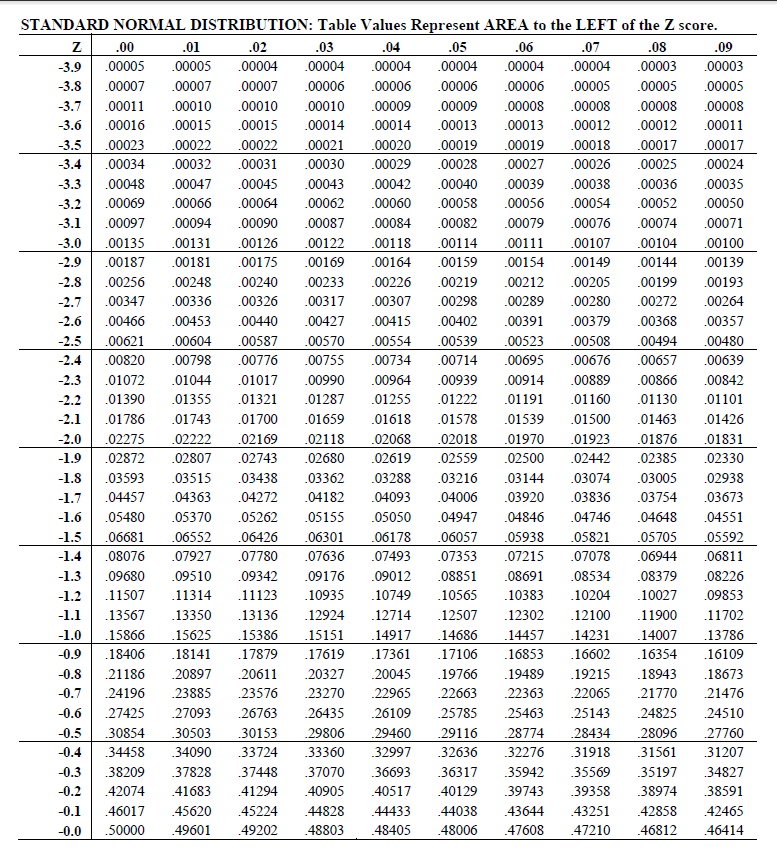
To read the value 1.57 on a typical table, go to 1.5 down and 0.07 across. Printed tables usually give cumulative probabilities, the chance that a statistic takes a value less than or equal to a number, from at least 0.00 to 2.99 by 1/100.
These can easily be checked by inspecting a number like 2.99: Cumulative from zero The cumulative probability, starting from 0: Prob (0 ≤ Z ≤ 1.57) =. Complementary cumulative The complement (1–x) of above: Prob(Z ≥ 1.57) =. Tables use at least 3 different conventions, depending on the interpretation of the meaning of an entry such as 1.57: Cumulative This is most common, and gives Prob(Z ≤ 1.57) = 0.9418.


 0 kommentar(er)
0 kommentar(er)
